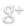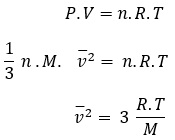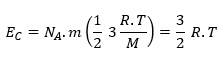En base a los temas desarrollados, se posee la información suficiente para desarrollar un modelo cuantitativo, desde el punto de vista microscópico y cinético, que sea útil para realizar predicciones y comprender el comportamiento de las moléculas.
Además, se explican determinadas propiedades macroscópicas que se correlacionan con el modelo.
La teoría cinética molecular se resume en los siguientes enunciados:
- Todo volumen macroscópico de gas está constituido por un gran numero de moleculas. Todas sus moléculas son idénticas si el gas es un elemento o compuesto estable.
- Las moléculas se encuentran separadas por distancias grandes, comparadas con sus propias dimensiones están en estado de continuo movimiento. El volumen ocupado por las moléculas es una fracción sumamente pequeña del volumen del recipiente.
- Las moléculas no ejercen fuerzas entre sí, excepto cuando chocan. Entre los choques con otras moléculas o con las paredes del recipiente, en cualquier instante, se mueven con amplia gama de velocidades y en línea recta.
- Los choques de las moléculas entre sí y con las paredes son perfectamente elasticos. Se considera que las paredes del recipiente son lisas y por lo tanto después del choque de las moléculas con las paredes no hay cambio de velocidad.
- En ausencia de fuerzas externas, las moleculas estan distribuidas uniformemente por todo el recipiente. Si N es el número total de moléculas en un recipiente de volumen V, el número de moléculas por unidad de volumen será N/V.
- Todas las direcciones de las velocidades moleculares son igualmente probables, ya que las moléculas tienen un movimiento aleatorio y obedecen las leyes del movimiento de Newton.
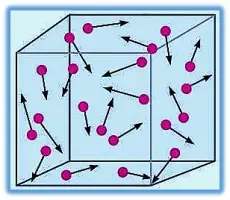
Si N es el número total de moléculas entonces Nv es el número de moléculas con velocidades comprendidas entre v y v+Δv. Este número es igual al área del rectángulo marcado con color amarillo en la siguiente imagen:
Vmp = velocidad mas probable
V = velocidad media
Vrms = velocidad cuadrática media
Se puede considerar que la distancia media entre moléculas de un gas ideal es grande comparada con el alcance de las fuerzas intermoleculares. Se puede representar un gas ideal como un conjunto de moléculas puntuales, donde las interacciones entre ellas se caracterizan por ser choques elásticos. Las moléculas se desplazan libremente en todas direcciones con velocidades diferentes como se representa en la primera imagen.
Para una muestra de un gas ideal compuesto por N moléculas encerradas en un recipiente de volumen V, se quiere evaluar la fuerza que ejercen las moléculas sobre las paredes del recipiente.
¿Cual es la fuerza que ejerce el gas en las paredes del recipiente por los choques múltiples de las moléculas?
La fuerza es: F = m.a donde m = masa del gas ; a = aceleración
Se considera una molécula moviéndose en la dirección x y reemplazando la aceleración en la expresión anterior:
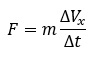Recordando que la velocidad v = d / t , y d es la distancia que se desplaza la molécula en la dirección x. Para N moléculas de gas:
Dado que en un gas las moléculas se mueven en todas direcciones con velocidades diferentes, para obtener la presión del gas, la velocidad debe ser sustituida por el promedio:
La velocidad molecular media es igual en todas direcciones. Por lo tanto, la velocidad media en la dirección x es igual a 1/3 de la velocidad molecular media.
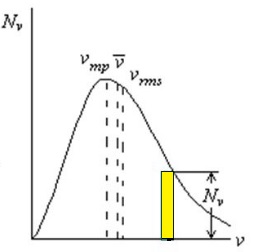
Recordando que la Presión (P) es igual al cociente entre la fuerza (F) y area (A): P = F/A . Siendo el volumen (V) igual al producto del área (A) por la distancia (d): V = A. d
El numero total de moléculas, N, es igual al número de moles, n, multiplicado por el numero de Avogadro: n.NA . Reemplazando en la ecuación anterior:
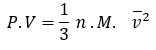Considerando la ecuación para un gas ideal:
Recordando la expresión para la energía cinética para N moléculas de gas:
Para 1 mol de gas ideal:
Para 1 molécula gaseosa:
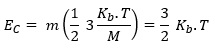Donde Kb es la constante de Boltzmann, su valor es 1,38×1023 J.(molécula.K)-1.
Es evidente que la temperatura de un gas es una medida de la energía cinética de las moléculas. Además, la presión del gas es proporcional al número de moléculas por unidad de volumen y de la energía cinética traslacional según la ecuación:
Se corrobora que la temperatura absoluta de un gas ideal es directamente proporcional a la energía cinética media de sus moléculas, sin importar a que presión y volumen se encuentren.
En promedio, las partículas tienen mayores energías cinéticas a mayor temperatura del gas. Es importante observar también que solo interviene la energía cinética de traslación y no otras energías como de rotación o vibración. La razón es que, en la sesión de cantidad de movimiento a las paredes solo contribuye el movimiento de traslación.
Un gas contiene una gran cantidad de moléculas con una distribución de velocidades. Por ello, no todas las partículas tienen la misma energía cinética sino que poseen una distribución de energías desde valores cercanos a cero hasta valores extremadamente grandes, Si cada partícula tuviera una temperatura asociada con su energía cinética, habría un amplio rango de temperaturas diferentes dentro del gas. Sin embargo esto no es así ya que en el equilibrio térmico el gas tiene una sola temperatura, que puede registrarse con un termómetro colocado dentro del gas. Así, la temperatura es una propiedad que caracteriza al gas globalmente.
El término velocidad promedio de la partícula y por ello la energía cinética promedio caracteriza a cada gas. Como la temperatura absoluta es proporcional a esta, no puede ser atribuida a cada partícula del gas individualmente. Se concluye entonces que no tiene sentido hablar de temperatura para cada molécula gaseosa.
Si dos gases ideales tienen la misma temperatura, la energía cinética promedio de cada una de las partículas del gas es la misma. Sin embargo, las velocidades promedio de las diferentes partículas no son las mismas, ya que las masa pueden ser diferentes.
Ley de distribución de Maxwell-Boltzmann
Si pudiera examinarse la distribución de las partículas en el espacio encontraríamos que se distribuyen por si solas entre estados de diferente energía de un modo específico que depende exponencialmente de la energía, tal fuera observado inicialmente por Maxwell y ampliado por Boltzmann.
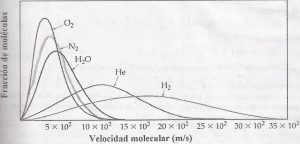
La ley de distribución de velocidades de Maxwell – Boltzmann muestra que las velocidades moleculares de un gas adquieren valores que dependen de la masa y la temperatura. A una dada temperatura, la fracción de partículas cuyas velocidades exceden un valor fijo aumenta a medida que la masa de las mismas disminuye; esto explica que las moléculas ligeras como el hidrógeno y helio puedan escapar más fácilmente de la atmósfera de la Tierra, mientras que las moléculas con mayor masa como el nitrógeno y el oxígeno permanecen en ella.
Inicialmente a una cierta temperatura, el número de moléculas aumenta conforme lo hace la velocidad hasta alcanzar un máximo, denominado velocidad mas probable, vpm. A partir de vmp, decrece asintóticamente hasta cero generando una curva de distribución no simétrica respecto a vmp; la menor velocidad debe ser cero y no hay un límite clásico a la mayor velocidad que pueda alcanzar una molécula.
Entonces la velocidad promedio, v, es algo mayor que vmp y la velocidad cuadrática media, vrms, al ser raíz cuadrada del promedio de la suma de los cuadrados de las velocidades, es aun mayor. El área bajo la curva de distribución (que es el número total de moléculas de la muestra del gas) sigue siendo la misma, entonces la distribución debe hacerse más plana a medida que la temperatura aumenta como se puede observar en la siguiente imagen.
Las moléculas gaseosas de mayor masa viajan a velocidades próximas a sus valores medios; las moléculas más livianas tienen valores de velocidades promedios más altas y su rango de velocidades es amplio (por eso la curva se suaviza).
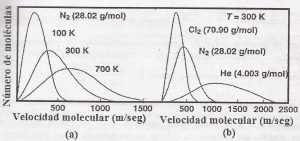
En la siguiente figura se presenta la variación de la velocidad con la temperatura y se observa el aumento en la gama de velocidades posibles a medida que se calienta el gas, se observa que la distribución se ensancha, lo que corresponde a una mayor distribución de velocidades. Esto explica los fenómenos de evaporacion y condensacion a partir de las velocidades de las moleculas.
Las partículas más livianas tienen velocidades tan altas que logran escapar con más facilidad; por ello el H2 y el He, son raros en la atmósfera terrestre.
